Recogeremos los datos y se realizará una tabla con todos ellos, posteriormente se puede representar por ejemplo en un diagrama de dispersión. Nuestro objetivo sera reconocer si hay relación entre las variables, de que tipo y si es posible el valor de una de ellas en función de la otra.
Tipos de disposiciones:
- Relación directa e inversa:
- Incorrelación
- Relación directa
- Relación inversa
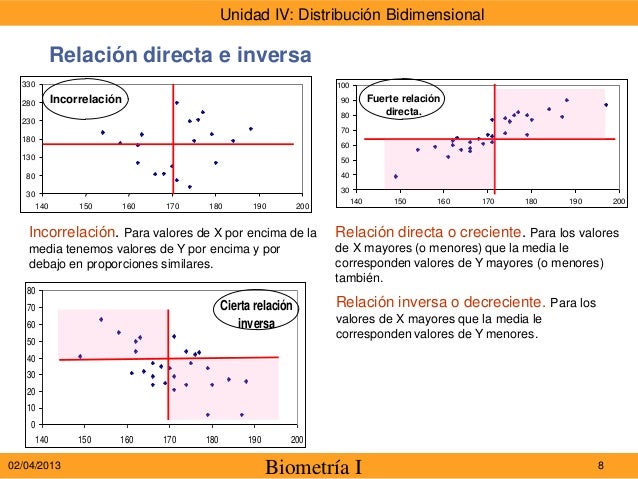
Relación variables independientes:
No hay relación
Relación variables dependientes:
-Funcional: puntos exactamente sobre la línea recta o curva.
-Estocástica: no están todos los puntos exactamente sobre el modelo, sino que existe una tendencia.

MODELOS DE ANÁLISIS DE REGRESIÓN
La regresión lineal simple estudia la asociación lineal entre dos variables cuantitativas.
y= a+ bx
A es el punto se inserción con el eje de coordenadas y b es la pendiente de la recta.
B expresa la cantidad de cambio que se produce en la variable dependiente por unidad de cambio en la independiente y A expresa el valor de la variable dependiente y cuando la independiente tiene valor cero.
Si b>0 hay relación directa, y si b<0 hay relación inversa.
Existen dos tipos de modelos:
- Determinista: la variable independiente determina el valor de la dependiente.
- Probabilísticos: por cada valor de la variable independiente existe una distribución de probabilidad de valores de la dependiente, con una probabilidad entre 0 y 1.
Los coeficientes de correlación son dos:
-Pearson: paramétricas por lo que requiere que la distribución siga la normalidad. Mide el grado de la relación de dependencia que existe entre las variables, cuyos valores van desde -1 hasta 1.
-Spearman: son no paramétricas por lo que requiere que se emplee cuando la distribución no sigue la normalidad. Es una medida de asociación que requiere que ambas variables en estudio sean medidas por lo menos en una escala ordinal.
Diferentes resultados para la regresión lineal simple:
A continuación dejo dos vídeos muy útiles sobre el coeficiente de correlación de Pearson y un ejercio:
Otro vídeo explicativo del coeficiente de correlación de spearman:
No hay comentarios:
Publicar un comentario